Enfoques y elementos de la probabilidad
- Experimento aleatorio o experimento: Cualquiera operación cuyo resultado no puede ser predicho con anterioridad con seguridad.
Ejemplo:
- Lanzamiento de una moneda.
- Lanzamiento de un dado.
- Extracción de una carta de una baraja de 52 cartas.
- Espacio muestral: es el conjunto de todos los posibles resultados asociados a un experimento. Su símbolo es la letra griega Ω (omega).Si el espacio muestral tiene un número finito de elementos o infinito numerable, entonces se dice que éste es discreto y si el espacio muestral tiene como elemento todos los puntos de algún intervalo real, entonces se dice que éste es continuo.
Ejemplos
- Experimento: lanzamiento de un dado
Ω = { 1, 2, 3, 4, 5, 6}
- Evento o suceso: es cualquier subconjunto de un espacio muestral. Todo subconjunto es un evento, en particular Ω mismo es un evento llamado suceso seguro y el conjunto vacío, Ø, también es un evento, llamado suceso imposible. Denotaremos a los eventos por las primeras letras del alfabeto en mayúsculas: A, B, C, etc.
Ejemplo:
- Cardinalidad del espacio muestral: corresponde a la cantidad de elementos contenidos en él.
Ejemplos:
A= {obtener un número impar al lanzar un dado}
A= {1, 3, 5}
B= {obtener al menos una cara al lanzar una moneda dos veces}
B= {cs, sc, cc}
Como los eventos son subconjuntos de Ω, entonces es posible alplicar la teoría de conjuntos para obtener nuevos eventos.
El complemento de un conjunto A se denota por Ac y se define como la colección de aquellos elementos de Ω que no pertenecen a A.
Si A y B son eventos, entonces también lo son A ∪ B, A ∩ B, Ac
A ∪ B ocurre sí, y solo si ocurre A o solo ocurre B u ocurren A y B a la vez.
A ∩ B ocurre si, y solo si ocurre A y ocurre B a la vez.
Ac ocurre si, y solo si no ocurre A
En todo esperimento aleatorio Ω se considera el conjunto universal, por lo tanto, todos los complementos son tomados respecto a Ω.
Video
Conjuntos
Un conjunto señala a la totalidad de los entes que tienen una propiedad común. Un conjunto está formado por una cantidad finita o infinita de elementos, cuyo orden es irrelevante. Los conjuntos matemáticos pueden definirse por extensión (enumerando uno a uno todos sus elementos) o por comprensión (se menciona sólo una característica común a todos los elementos)
Es posible realizar ciertas operaciones básicas que permiten hallar conjuntos dentro de otros:
unión: se simboliza con una especie de U, y se trata del conjunto formado por los elementos que pertenezcan a cualquiera de los conjuntos que se propongan para unión (en el caso de A y B, el conjunto resultante será A U B);
intersección: su símbolo es similar a una U rotada 180° y permite hallar los elementos que tienen en común los conjuntos dados;
diferencia: partiendo de los conjuntos A y B, su diferencia será el conjunto A \, formado por los elementos que solo se encuentren en A;
complemento: si un conjunto U contiene uno de nombre A, entonces el complemento de este último será aquel que contenga los elementos que no pertenecen a A;
Diagrama de venn
Un diagrama de Venn usa círculos que se superponen u otras figuras para ilustrar las relaciones lógicas entre dos o más conjuntos de elementos. A menudo, se utilizan para organizar cosas de forma gráfica, destacando en qué se parecen y difieren los elementos. Los diagramas de Venn, también denominados "diagramas de conjunto" o "diagramas lógicos", se usan ampliamente en las áreas de matemática, estadística, lógica, enseñanza, lingüística, informática y negocios. Muchas personas los vieron por primera vez en la escuela cuando estudiaron Matemática o Lógica, ya que los diagramas de Venn se convirtieron en una parte del plan de estudio de la "nueva Matemática" en la década de 1960. Estos pueden ser diagramas sencillos que involucran dos o tres conjuntos con algunos elementos o pueden volverse muy sofisticados, por ejemplo, en presentaciones en 3D, ya que utilizan seis o siete conjuntos o más. Se usan para hacer un análisis detallado y para representar cómo se relacionan los elementos entre sí dentro de un "universo" o segmento determinado. Los diagramas de Venn permiten a los usuarios visualizar los datos de forma clara y con gran alcance y, por este motivo, se utilizan comúnmente en presentaciones e informes. Se relacionan estrechamente con los diagramas de Euler, pero se diferencian en que estos últimos omiten los conjuntos si estos no contienen elementos. Los diagramas de Venn muestran las relaciones incluso si un conjunto está vacío.
Ejemplos


Video
Técnicas de conteo
Diagrama de arbol
Un diagrama de árbol es una representación gráfica que muestra los resultados posibles de una serie de experimentos y sus respectivas probabilidades; consta de r pasos, donde cada uno de los pasos tiene un número finito de maneras de ser llevado a cabo.
Para la construcción de un diagrama en árbol se partirá poniendo una rama para cada una de las posibilidades, acompañada de su probabilidad. En el final de cada rama parcial se constituye a su vez, un nudo del cual parten nuevas ramas, según las posibilidades del siguiente paso, salvo si el nudo representa un posible final del experimento (nudo final). Hay que tener en cuenta: que la suma de probabilidades de las ramas de cada nudo ha de dar 1.
Los diagramas en árbol son muy útiles para "fabricar" cualquier tipo de agrupación, ya sean variaciones, permutaciones o combinaciones.
Video
Principio de permutación
A diferencia de la formula de la multiplicación, se la utiliza para determinar el numero de posibles arreglos cuando solo hay un solo grupo de objetos. Permutación: un arreglos o posición de r objetos seleccionados de un solo grupo de n objetos posibles. Si nos damos cuenta los arreglos a, b, c y b, a, c son permutaciones diferentes, la formula que se utiliza para contar el numero total de permutaciones distintas es:
FÓRMULA: n P r = n! (n - r)
Ejemplo
¿Como se puede designar los cuatro primeros lugares de un concurso, donde existen 15 participantes?
Aplicando la formula de la permutación tenemos:
n P r = n! (n - r)! = 15! = 15*14*13*12 *11*10*9*8*7*6*5*4*3*2*1 (15-4)! 11*10*9*8*7*6*5*4*3*2*1 = 32760
Donde: n= número total de objetos r= número de objetos seleccionados!= factorial, producto de los números naturales entre 1 y n.
NOTA: se puede cancelar números cuando se tiene las mismas cifras en numerador y denominador. !
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:
Permutaciones: AB, AC, BA, CA, BC, CB
Combinaciones: AB, AC, BC
Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.
La fórmula de combinaciones es:
n C r = n! r! (n – r)!
Ejemplo: En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?
Usando la fórmula de combinaciones:
n C r = n! = 7! = 7! = 35
r! (n – r )! 3! (7 – 3)! 3! 4!
El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.
Si se desea realizar una actividad que consta de r pasos, en donde el primer paso de la actividad a realizar puede ser llevado a cabo de N1 maneras o formas, el segundo paso de N2 maneras o formas y el r-ésimo paso de Nr maneras o formas, entonces esta actividad puede ser llevada a efecto de. El principio multiplicativo implica que cada uno de los pasos de la actividad deben ser llevados a efecto, uno tras otro. Si un evento E1 puede suceder de n1 maneras diferentes, el evento E2 puede ocurrir de n2 maneras diferentes, y así sucesivamente hasta el evento Ep el cual puede ocurrir de np maneras diferentes, entonces el total de maneras distintas en que puede suceder el evento “ocurren E1 y E2…..y Ep” es igual a producto.
N1 x N2 x ..........x Nr maneras o formas
Ejemplo
Se dispone de 3 vías para viajar de C1 a C2 y de 4 vías para viajar de C2 a C1. ¿De cuántas formas se puede organizar el viaje de ida y vuelta de C1 a C2.Respuesta: (3)(4)=12
Si se desea llevar a efecto una actividad, la cuál tiene formas alternativas para ser realizada, donde la primera de esas alternativas puede ser realizada de M maneras o formas, la segunda alternativa puede realizarse de N maneras o formas ..... y la última de las alternativas puede ser realizada de W maneras o formas, entonces esa actividad puede ser llevada a cabo de,
M + N + .........+ W maneras o formas
Ejemplos:
1) Una persona desea comprar una lavadora de ropa, para lo cuál ha pensado que puede seleccionar de entre las marcas Whirpool, Easy y General Electric, cuando acude a hacer la compra se encuentra que la lavadora de la marca W se presenta en dos tipos de carga ( 8 u 11 kilogramos), en cuatro colores diferentes y puede ser automática o semiautomática, mientras que la lavadora de la marca E, se presenta en tres tipos de carga (8, 11 o 15 kilogramos), en dos colores diferentes y puede ser automática o semiautomática y la lavadora de la marca GE, se presenta en solo un tipo de carga, que es de 11 kilogramos, dos colores diferentes y solo hay semiautomática. ¿Cuántas maneras tiene esta persona de comprar una lavadora?
Solución:
M = Número de maneras de seleccionar una lavadora Whirpool
N = Número de maneras de seleccionar una lavadora de la marca Easy
W = Número de maneras de seleccionar una lavadora de la marca General Electric
M = 2 x 4 x 2 = 16 maneras
N = 3 x 2 x 2 = 12 maneras
W = 1 x 2 x 1 = 2 maneras
M + N + W = 16 + 12 + 2 = 30 maneras de seleccionar una lavadora.
Eventos mutuamente excluyentes:
son dos resultados de un evento que no pueden ocurrir al mismo tiempo.
Ejemplo
- Sacar una carta de un mazo estándar y que salga un as y un rey son eventos mutuamente excluyentes, ya que no pueden ocurrir los dos al mismo tiempo.
- Sin embargo, sacar una carta roja y rey no son eventos mutuamente excluyentes, ya que puedes sacar perfectamente un rey rojo
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Dos o más eventos son independientes cuando la ocurrencia o no-ocurrencia de un evento no tiene efecto sobre la probabilidad de ocurrencia del otro evento (o eventos). Un caso típico de eventos independiente es el muestreo con reposición, es decir, una vez tomada la muestra se regresa de nuevo a la población donde se obtuvo.
Ejemplo:
lanzar al aire dos veces una moneda son eventos independientes por que el resultado del primer evento no afecta sobre las probabilidades efectivas de que ocurra cara o sello, en el segundo lanzamiento
Video
BLOQUE 2
Distribución de Bernoulli
La distribución de Bernoulli cuando un proceso aleatorio tenga exactamente dos resultados: evento o no evento. Por ejemplo, en el campo de la calidad, un producto se puede clasificar como bueno o malo.
Las variables de Bernoulli pueden tomar dos valores numéricos, 0 y 1, donde 1 corresponde a un evento y 0 corresponde a un no evento. Una variable aleatoria X sigue una distribución de Bernoulli si P(X = 1) = p y P(X = 0) = 1 – p, donde p es la probabilidad de ocurrencia del evento.
La distribución de Bernoulli es una distribución discreta que está relacionada con muchas distribuciones, tales como la distribución binomial, geométrica y binomial negativa. La distribución de Bernoulli representa el resultado de 1 ensayo. Las secuencias de ensayos de Bernoulli independientes generan las demás distribuciones
Ejemplo
Video
Distribución binomial
Una distribución binomial es una distribución discreta que modela el número de eventos en un número de ensayos fijo. Cada ensayo tiene dos resultados posibles, y evento es el resultado de interés en un ensayo.
Utilice la distribución binomial para describir un proceso donde los resultados se pueden etiquetar como un evento o un no evento y cuando esté interesado en la ocurrencia de un evento y no en su magnitud.
Ejemplo
Un elemento pasa o no pasa una inspección o un partido político gana o pierde. La distribución binomial se usa frecuentemente en control de calidad, sondeos de opinión pública, investigaciones médicas y seguros.
Utilice la distribución binomial para calcular la probabilidad de que 3 o más elementos defectuosos se encuentren en una muestra de 25 elementos si la probabilidad de un elemento defectuoso en cada ensayo es 0.02. El número de elementos defectuosos (X) sigue una distribución binomial con n = 25 y p = 0.02.
El número de eventos (X) en n ensayos sigue una distribución binomial si se cumplen las siguientes condiciones:
- El número de ensayos es fijo.
- Cada ensayo es independiente de otros ensayos.
- Cada ensayo tiene uno de dos resultados: evento o no evento.
- La probabilidad de un evento es igual para cada ensayo.
Una de las propiedades de la distribución binomial es que cuando n es grande, la distribución binomial puede ser aproximada razonablemente por la distribución normal. Por ejemplo, para la siguiente distribución binomial
Video
Función de densidad de probabilidad para la variable aleatoria continua. Fue descubierta por Carl Gauss al estudiar el comportamiento de los procesos aleatorios. Es ampliamente utilizada en estadística y teoría de las probabilidades.
La función asociada a la distribución normal está dada por:
Donde: μ: media de la distribución.
σ: desviación estándar de la distribución.
π = 3.1415926535…
x: variable aleatoria.
σ: desviación estándar de la distribución.
π = 3.1415926535…
x: variable aleatoria.
A una distribución normal de media μ y desviación estándar σse le denota N(μ,σ).
La distribución normal cuando μ= 0 y σ = 1 recibe el nombre de curva normal unitaria (N(0,1)).
Existe una función matemática, con forma de campana que tiene la siguiente definición:
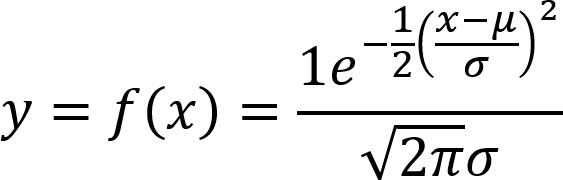
Si se grafica esta función, se obtiene como resultado la curva normal:

Además, tiene las siguientes características:
- Toma en cuenta la media(µ) y la desviación estándar(σ).
- El área bajo la curva es igual a uno.
- Es simétrica respecto al centro, o a la media.
- 50% de los valores son mayores que la media, y 50% de los valores son menores que la media.
- La media es igual a la mediana y a la moda.
- Tiene una asíntota en y = 0 (eje x).
Algunos otros ejemplos de variables con distribución normal:
- Notas en un examen.
- Errores de medida.
- Presión sanguínea.
- Tamaño de las piezas producidas por una máquina.
Para encontrar las probabilidades o cantidad de datos entre determinados valores de la variable, se calcula el área bajo la curva normal, que se encuentra en la tabla z o tabla de áreas bajo la curva normal estandarizada.
La distribución normal estándar
La distribución normal estándar, es aquella distribución normal que tiene una media igual a cero, y una desviación estándar igual a uno.Veamos la función densidad normal estandarizada, que trabaja con la variable estandarizada z en el eje horizontal:

Ejemplo
si se desea encontrar la probabilidad de que la variable estandarizada z, tome un valor entre 0 y 1,50; hay que encontrar el área bajo la curva entre z = 0 y z = 1,50.

Para calcular el valor de esta área, se utiliza la tabla z y se busca el valor de 1,50:

Como vemos, el valor del área bajo la curva es de 0,4332, y esa sería la probabilidad de que la variable estandarizada z, tome un valor comprendido entre 0 y 1,50.
Vídeo
BLOQUE 3
Probabilidad condicional
es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribe P(A|B) o P(A/B), y se lee «la probabilidad de A dado B».
No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. Apuede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no, dependiendo de la interpretación que se le dé a los eventos.
Ejemplo:
Se seleccionan dos semillas aleatoriamente, una por una, de una bolsa que contiene 10 semillas de flores rojas y 5 de flores blancas. ¿Cuál es la probabilidad de que:
- La primera semilla sea roja?
- La segunda semilla sea blanca dado que la primera fue roja?
Solución:
- La probabilidad de que la primera semilla sea roja es puesto que hay 10 semillas de flores rojas de un total de 15. Escrito con notación de probabilidad tenemos:
- La probabilidad de que la segunda semilla sea blanca se ve influida por lo que salió primero, es decir esta probabilidad está sujeta a una condición, la de que la primera semilla sea roja. Este tipo de probabilidad se le llama probabilidad condicional y se denota por
, y se lee: la probabilidad de B2dado R1.
Esta probabilidad puesto que todavía hay 5 semillas blancas en un total de 14 restantes.
Vídeo
El teorema de Bayes
Es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.
Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad. El teorema de Bayes entiende la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionado a B.
Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla. Para demostrarlo, utilizaremos un ejemplo en el que en lugar de A(1), A(2) y A(3), utilizaremos directamente A, B y C.
Ejemplo del teorema de Bayes
Una empresa tiene una fábrica en Estados Unidos que dispone de tres máquinas A, B y C, que producen envases para botellas de agua. Se sabe que la máquina A produce un 40% de la cantidad total, la máquina B un 30% , y la máquina C un 30%. También se sabe que cada máquina produce envases defectuosos. De tal manera que la máquina A produce un 2% de envases defectuosos sobre el total de su producción, la máquina B un 3%, y la máquina C un 5%. Dicho esto, se plantean dos cuestiones:
1.Si un envase ha sido fabricado por la fábrica de esta empresa en Estados Unidos ¿Cuál es la probabilidad de que sea defectuoso?
Se calcula la probabilidad total. Ya que, a partir los diferentes sucesos, calculamos la probabilidad de que sea defectuoso
P(D) =[ P(A) x P(D/A) ] + [ P(B) x P(D/B) ] + [ P(C) x P(D/C) ] = [ 0,4 x 0,02 ] + [ 0,3 x 0,03 ] + [ 0,3 x 0,05 ] = 0,032
Expresado en porcentaje, diríamos que la probabilidad de que un envase fabricado por la fábrica de esta empresa en Estados Unidos sea defectuoso es del 3,2%.
2. Siguiendo con la pregunta anterior, si se adquiere un envase y este es defectuoso ¿Cuáles es la probabilidad de que haya sido fabricado por la máquina A?¿Y por la máquina B?¿Y por la máquina C?
Aquí se utiliza el teorema de Bayes. Tenemos información previa, es decir, sabemos que el envase es defectuoso. Claro que, sabiendo que es defectuoso, queremos saber cual es la probabilidad de que se haya producido por una de las máquinas.
P(A/D) = [P(A) x P(D/A)] / P(D) = [0,40 x 0,02] / 0,032 = 0,25
P(B/D) = [P(B) x P(D/B)] / P(D) = [0,30 x 0,03] / 0,032 = 0,28
P(C/D) = [P(C) x P(D/C)] / P(D) = [0,30 x 0,05] / 0,032 = 0,47
Sabiendo que un envase es defectuoso, la probabilidad de que haya sido producido por la máquina A es del 25%, de que haya sido producido por la máquina B es del 28% y de que haya sido producido por la máquina C es del 47%
Video
Distribución de Poisson
La distribución de Poisson se especifica por un parámetro: lambda (λ). Este parámetro es igual a la media y la varianza. Cuando lambda aumente a valores lo suficientemente grandes, la distribución normal (λ, λ) podría utilizarse para aproximar la distribución de Poisson.
Utilice la distribución de Poisson para describir el número de veces que un evento ocurre en un espacio finito de observación. Por ejemplo, una distribución de Poisson puede describir el número de defectos en el sistema mecánico de un avión o el número de llamadas a un centro de llamadas en una hora. La distribución de Poisson se utiliza con frecuencia en el control de calidad, los estudios de fiabilidad/supervivencia y los seguros.
Una variable sigue una distribución de Poisson si se cumplen las siguientes condiciones:
- Los datos son conteos de eventos (enteros no negativos, sin límite superior).
- Todos los eventos son independientes.
- La tasa promedio no cambia durante el período de interés.
Las siguientes gráficas representan distribuciones de Poisson con valores diferentes de lambda.

Lambda = 3

Lambda = 10
¿Qué es tasa de ocurrencia?
La tasa de ocurrencia es igual a la media (λ) dividida entre la dimensión del espacio de observación. Es útil para comparar conteos de Poisson recolectados en diferentes espacios de observación. Por ejemplo, la central telefónica A recibe 50 llamadas telefónicas en 5 horas y la central telefónica B recibe 80 llamadas en 10 horas. Usted no puede comparar directamente estos valores, porque sus espacios de observación son diferentes. Debe calcular la tasa de ocurrencia para comparar estos conteos. La tasa de la central telefónica A es (50 llamadas / 5 horas) = 10 llamadas/hora. La tasa de la central telefónica B es (80 llamadas / 10 horas) = 8 llamadas/hora.
Diferencias entre la distribución de Poisson y la distribución binomial
La distribución de Poisson es similar a la distribución binomial porque ambas modelan conteos de eventos. Sin embargo, dentro de su espacio de observación finito, la distribución de Poisson no establece un límite superior a este conteo: una central telefónica podría recibir un número ilimitado de llamadas en un día y no violar los requisitos de la distribución de Poisson. En cambio, la distribución binomial establece un límite superior en el conteo: el número de eventos que usted observa no puede exceder el número de ensayos que realiza.
Vídeo:
- Obtener vínculo
- X
- Correo electrónico
- Otras apps
- Obtener vínculo
- X
- Correo electrónico
- Otras apps
















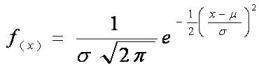


Comentarios